Lesson 2 感知机

发表于 分类于 阅读次数：

1．感知机是根据输入实例的特征向量$x$对其进行二类分类的线性分类模型：

$$f(x)=\operatorname{sign}(w \cdot x+b)$$

感知机模型对应于输入空间（特征空间）中的分离超平面 $w \cdot x+b=0$。

2．感知机学习的策略是极小化损失函数：

$$\min_{w,b}L(w,b)=-\sum_{x_i\in M}y_i(w\cdot x_i+b)$$

损失函数对应于误分类点到分离超平面的总距离。

3．感知机学习算法是基于随机梯度下降法的对损失函数的最优化算法，有原始形式和对偶形式。算法简单且易于实现。原始形式中，首先任意选取一个超平面，然后用梯度下降法不断极小化目标函数。在这个过程中一次随机选取一个误分类点使其梯度下降。

4．当训练数据集线性可分时，感知机学习算法是收敛的。感知机算法在训练数据集上的误分类次数$k$满足不等式：

$$k \leqslant\left(\frac{R}{\gamma}\right)^{2}$$

当训练数据集线性可分时，感知机学习算法存在无穷多个解，其解由于不同的初值或不同的迭代顺序而可能有所不同。

二分类模型

$$f(x) = sign(w\cdot x + b)$$

$$\left.\mathrm{sign}(x)=\left\lbrace\begin{aligned}&+1,x\geqslant0 \\ &-1,x<0\end{aligned}\right.\right.$$

给定训练集：
$$T=\lbrace (x_{1}, y_{1}),(x_{2}, y_{2}), \cdots,(x_{N}, y_{N})\rbrace$$

定义感知机的损失函数

$$L(w, b)=-\sum_{x_{i} \in M} y_{i}(w \cdot x_{i}+b)$$

算法

随即梯度下降法 (Stochastic Gradient Descent),随机抽取一个误分类点使其梯度下降。

$$w = w + \eta y_{i}x_{i}$$

$$b = b + \eta y_{i}$$

当实例点被误分类，即位于分离超平面的错误侧，则调整 $w$, $b$ 的值，使分离超平面向该无分类点的一侧移动，直至误分类点被正确分类

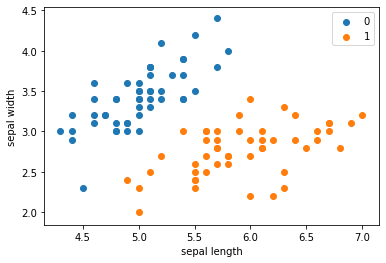
拿出iris数据集中两个分类的数据和 [sepal length，sepal width] 作为特征

1
2
3
4
5
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
# matplotlib inline
1
2
3
4
5
6
7
8
# load data
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
# print(df)

df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
df.label.value_counts()
1
2
3
4
5
6
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
# plt.scatter(df[100:150]['sepal length'], df[100:150]['sepal width'], label='2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

image.png

1
2
3
data = np.array(df.iloc[:100, [0, 1, -1]])  #iloc 是pandas的函数
X, y = data[:,:-1], data[:,-1]
y = np.array([1 if i == 1 else -1 for i in y])

Perceptron

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 数据线性可分，二分类数据
# 此处为一元一次线性方程
class Model:
    def __init__(self):
        self.w = np.ones(len(data[0]) - 1, dtype=np.float32)
        self.b = 0
        self.l_rate = 0.1
        # self.data = data

    def sign(self, x, w, b):
        y = np.dot(x, w) + b   # np.dot（）向量点乘
        return y

    # 随机梯度下降法
    def fit(self, X_train, y_train):
        is_wrong = False
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train)):
                X = X_train[d]
                y = y_train[d]
                if y * self.sign(X, self.w, self.b) <= 0:
                    self.w = self.w + self.l_rate * np.dot(y, X)
                    self.b = self.b + self.l_rate * y
                    wrong_count += 1
            if wrong_count == 0:
                is_wrong = True
        return 'Perceptron Model!'

    def score(self):
        pass
1
2
3
4
5
6
7
8
9
10
11
12
perceptron = Model()
perceptron.fit(X, y)

x_points = np.linspace(4, 7, 10)
y_ = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1]
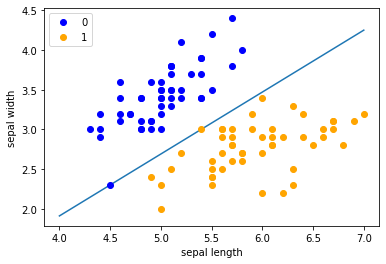
plt.plot(x_points, y_)

plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

image-1.png

scikit-learn实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import sklearn
from sklearn.linear_model import Perceptron

clf = Perceptron(penalty="l2",max_iter=1000, shuffle=True)
clf.fit(X, y)

# Weights assigned to the features.分配给特征的权重。
print(clf.coef_)  

# 截距 Constants in decision function.决策函数中的常量。
print(clf.intercept_)

# 画布大小
plt.figure(figsize=(10,10))

# 中文标题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.title('鸢尾花线性数据示例')

plt.scatter(data[:50, 0], data[:50, 1], c='b', label='Iris-setosa',)
plt.scatter(data[50:100, 0], data[50:100, 1], c='orange', label='Iris-versicolor')

# 画感知机的线
x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
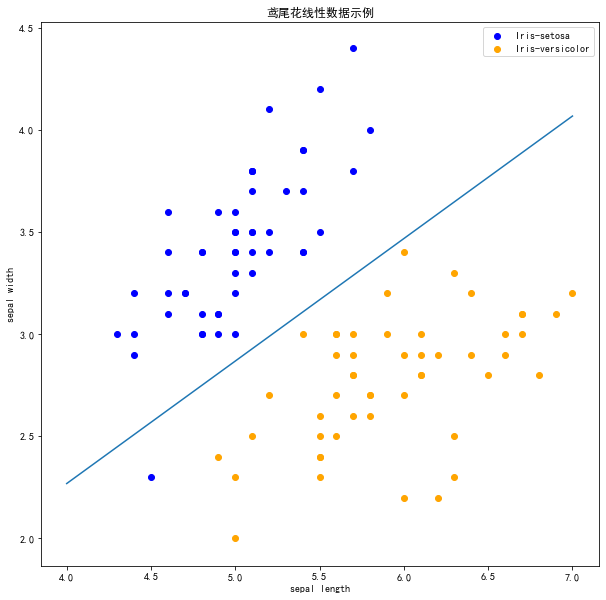
plt.plot(x_ponits, y_)

# 其他部分
plt.legend()  # 显示图例
plt.grid(False)  # 不显示网格
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

image-2.png

sklearn.linear_model.Perceptron(*, penalty=None, alpha=0.0001, fit_intercept=True, max_iter=1000, tol=0.001, shuffle=True, verbose=0, eta0=1.0, n_jobs=None, random_state=0, early_stopping=False, validation_fraction=0.1, n_iter_no_change=5, class_weight=None, warm_start=False)

  1. penalty{‘l2’,’l1’,’elasticnet’}, default=None
    要使用的惩罚函数(也称为正规化格式)。

  2. alphafloat, default=0.0001
    在使用正则化的情况下乘以正则化项的常量。

  3. fit_interceptbool, default=True
    是否应该估计截距。如果为False，则认为数据已经居中。

  4. max_iterint, default=1000
    通过训练数据的最大次数(即epochs)。它只影响fit方法中的行为，而不影响partial_fit方法。(New in version 0.19.)

  5. tolfloat, default=1e-3
    停止准则。如果不为空，迭代将在(loss > previous_loss - tol)时停止。(New in version 0.19.)

  6. shufflebool, default=True
    训练数据是否在每个迭代之后进行重新排列。

  7. verboseint, default=0
    The verbosity level

  8. eta0double, default=1
    更新相乘的常数(学习率)

注意 !

在上图中，有一个位于左下角的蓝点没有被正确分类，这是因为 SKlearn 的 Perceptron 实例中有一个tol参数。

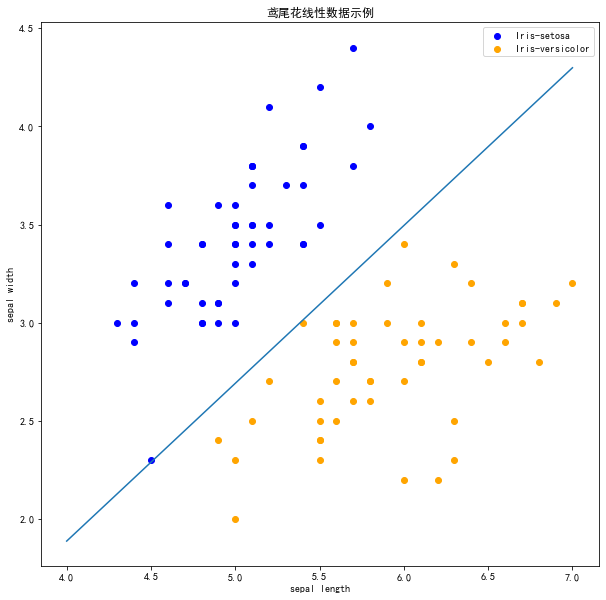
tol 参数规定了如果本次迭代的损失和上次迭代的损失之差小于一个特定值时，停止迭代。所以我们需要设置 tol=None 使之可以继续迭代：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
clf = Perceptron(fit_intercept=True, max_iter=1000,tol=None,shuffle=True)
clf.fit(X, y)

# 画布大小
plt.figure(figsize=(10,10))

# 中文标题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.title('鸢尾花线性数据示例')

plt.scatter(data[:50, 0], data[:50, 1], c='b', label='Iris-setosa',)
plt.scatter(data[50:100, 0], data[50:100, 1], c='orange', label='Iris-versicolor')

# 画感知机的线
x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)

# 其他部分
plt.legend()  # 显示图例
plt.grid(False)  # 不显示网格
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

image-3.png